• 1: Greek Geometry
• 2: Co-ordinate geometry
• 3: Trigonometry I
• 4: Quadratics
• 5: Circles
• 6: Trigonometry II
• 7: Polynomials
• 8: Sequences & Recurrence Relations

1: Greek Geometry

• Pythagoras theorem
• geometric demonstration of expansion of `(x+y)^2`
• methodology (proof)
• revision of expansion of brackets algebraically
• concepts of congruence and similarity

1: Greek Geometry

1: Greek Geometry

1.1 Pythagoras Theorem

In any right-angled triangle the side lengths satisfy

`x^2 + y^2 = z^2`

Example

What is the exact length of `AB` and what is the length to 2 d.p.

`AB^2 = 8^2+3^2 = 64+9=73`

So `AB = sqrt(73) quad quad `(exact length)
and `AB=8.54 quad quad` (2d.p.)

Proof of Pythagoras Theorem

The two square diagrams have the same area. Also the shaded triangles in the diagrams have the same area.

Unshaded area in the two diagrams is the same

So `z^2 = x^2 + y^2`

1.2 Algebraic aside

The unshaded area in the diagram on the left is `x^2 + y^2` and the unshaded area in the diagram on the right is the area of the whole square; that is `(x+y)^2`.

Unshaded area in the two diagrams is different!

So `x^2 + y^2` is different to `(x+y)^2`

Algebraic explanation

Formula is `(x+y)^2 = x^2+2xy+y^2` `quad quad (**)`

Can show this is the case by expanding `(x+y)^2`

LHS` = (x+y)^2 = (x+y)(x+y)`

`=x(x+y)+y(x+y)`

`=x^2+xy+yx+y^2`

`=x^2+2xy+y^2 = ` RHS

RHS of `(**)` is called the expansion of `(x+y)^2`

Useful formula `(a-b)(a+b)=a^2-b^2` `quad quad (** **)`

Explanation:

`(a-b)(a+b)=a(a+b)-b(a+b)`

`=a^2+ab-ba-b^2`

`=a^2-b^2`

Exercise

1. Check `(** **)` when `a=5` and `b=4`
2. Expand `(x-6)(x+6)`

1.3 Geometric Aside

Area of a triangle `= 1/2 ("base" times "height")`

Reason

True for right-angled triangle because its area is `1/2 times "area of rectangle"`.

But any triangle can be split into two right angled triangles.

So area of triangle

`= 1/2 ah + 1/2bh =1/2(a+b)h`

`=1/2("base" times "height")`

1.4 Similarity and Congruence

Two figures (e.g. squares, triangles, diagrams, etc.) are similar if one is just a scaled up version of the other.

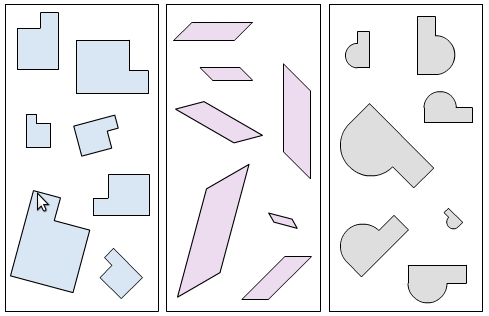
For example, in each box to the right the shapes are similar to each other.

Similar figures have the same shape but differ in size.

Corresponding sides scale up or down by the same proportions.

Similar Triangles

The triangles `ABC` and `DEF` are similar if, and only if, the angles are the same.

Then we have

• `AB = k times DE`
• `BC = k times EF`
• `AC = k times DF`

where `k` is the scaling factor.

Example

Triangles `ABC` and `ADE` are similar.

1. If the length of AD is `12` cm, find the length of `DE`.
2. If `Ahat(C)B = 60^circ` what is `Ahat(E)D`.

1. Since they are similar `AB=k times AD` and `BC= k times DE`. So
   `k = frac(AB)(AD) = frac(9)(12) = frac(3)(4)` and `6 = frac(3)(4) times DE`. Thus, `DE = frac(24)(3) = 8` cm
2. `Ahat(C)B = 60^circ` tells us that `Ahat(E)D = 60^circ`.

Exercises

1. `ABCD` and `PQRS` are similar rectangles.
1. Find the length of `RS`.
2. Write down the length of `QP`.
2. Triangles `ADE` and `ABC` are similar.  Find the length of `AB`.
3. Triangles `ABC` and `ADE` are similar.  Find the length of `AC`.

Congruence

Two figures are congruent if they are the same apart from their positioning in the plane i.e. they are similar with scaling factor `1`.

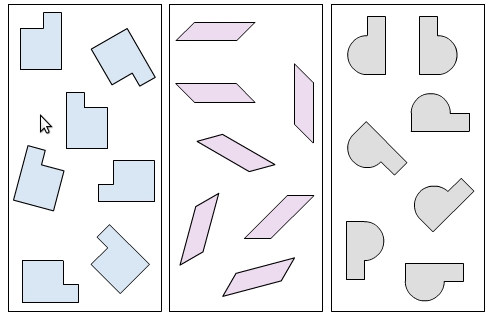
For example, in each box to the right the shapes are congruent to each other.

Congruence

Example

A diagonal of a parallelogram divides the parallelogram into two triangles which are congruent to each other.

Exercise: True or False?

• 1. All squares are congruent.
• 2. All circles are similar.
• 3. Angles in similar shapes are always the same.
• 4. All pairs of similar shapes are congruent.