James Gray
University of Edinburgh
Applicable Mathematics (Foundation) af0
3: Trigonometry
3.1 sin, cos and tan
`theta` is an angle between `0^circ` and `90^circ`. Draw a right-angled
triangle with `theta` as one of the angles. Any two such triangles will be
similar so the ratio of the sides of the triangle will be the same.

3.1 sin, cos and tan
Can define:
- `sin theta = "opposite"/"hypotenuse"`
- `cos theta = "adjacent"/"hypotenuse"`
- `tan theta = "opposite"/"adjacent"`
Often remembered by: soh-cah-toa
Note
sin, cos and tan are abbreviations of sine, cosine and tangent.
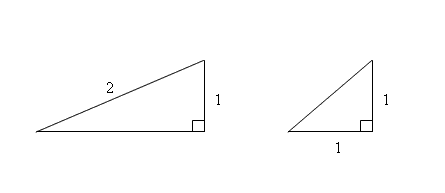
3.2 Special Cases
Need to know these triangles for exact values of sin, cos and tan with the angles
`30^circ`, `45^circ` and `60^circ`.
Example
Q: A surveyor stands 25m from a building and measures the angle to the top
from the horizontal to be `30^circ`. How high is the building?
A:
- `"height"/25 = tan 30^circ= 1/sqrt(3)`
- `"height" = 25/sqrt(3) "m" qquad qquad "(exact answer)"`
- `"height" = 14.4 "m" qquad qquad "(1 d.p.)"`
Exercises
- Sine / Cosine / Tangent: H p337; Ex 14
- Special Angles: H p57; Ex 4D
- Special Angles: H p59; Ex 4E
3.3 Radians
An angle has size `theta` radians if the arc it subtends on the circumference of
a circle of radius `1` has length `theta` units.
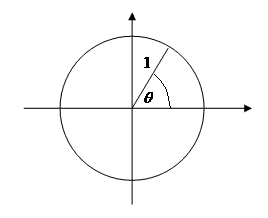
Circumference of circle of radius `1` is `2pi`. So we have
- `180^circ = pi \ \ "radians"`
In general
- `theta^circ = theta / (180) pi \ \ "radians"`
- `x \ \ "radians" = x/(pi) times 180^circ`
So:
|
Degrees |
`360^circ` |
`180^circ` |
`90^circ` |
`60^circ` |
`45^circ` |
`30^circ` |
|
Radians |
`2pi` |
`pi` |
`pi/2` |
`pi/3` |
`pi/4` |
`pi/6` |
Notes
- No symbol means angle is in radians e.g.
- `sin 10` means sine of 10 radians
- `sin 10^circ` means sine of 10 degrees
- In calculus (i.e. the mf0 course) angles are usually measured in radians.
Exercises
- Radians: H p56; Ex 4C
- Sine / Cosine / Tangent: H p337; Ex 14
- Special Angles: H p57; Ex 4D
- Special Angles: H p59; Ex 4E
3.4 Trigonometry for any angle
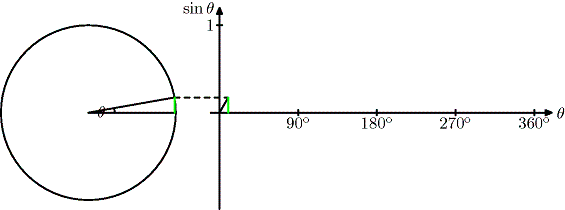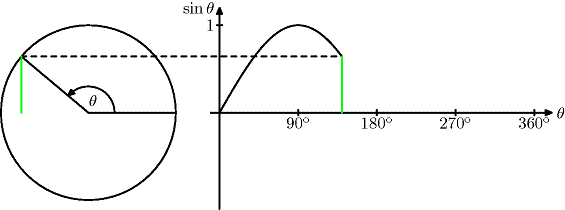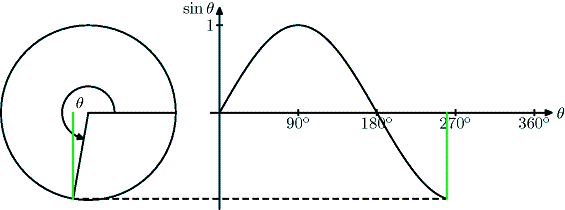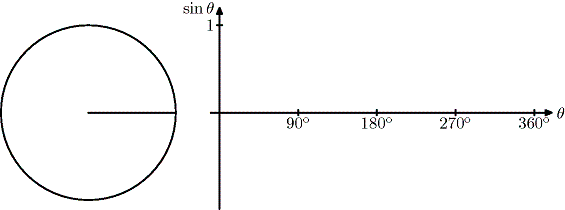
Draw a circle radius 1. The point P which lies on the circle
has coordinates `(cos theta, sin theta)`.

We define `tan theta = (sin theta)/(cos theta)`
Example
Q: What is the exact value of `sin 300^circ`?
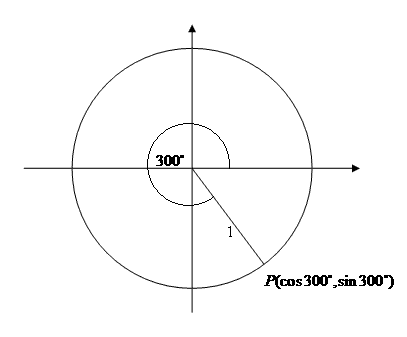
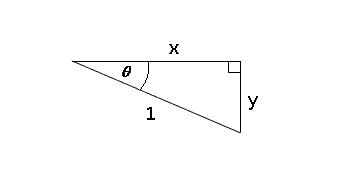
A: The coordinates of the point `P` are `(cos 300^circ , sin 300^circ)` so we need
to find the values for these. Draw in a triangle between the `x`-axis and
the point `P`.
We deduce that the angle `theta = (360 - 300)^{circ} = 60^{circ}`. Using our standard triangles we find that `x =
1/2` and `y=sqrt(3)/2`.
Hence the coordinates of `P` are `(1/2, - sqrt(3)/2)`. Thus we have found that
- `sin 300^circ = - sqrt(3)/2`
Note
- Positive angles are measured anti-clockwise
- Negative angles are measured clockwise

N.B. Anti-clockwise is defined to be positive as this is the way we think of the Earth rotating (from the
persperctive of the Northern hemisphere).
Right-hand Rule: Hold you right hand out in front of you with your thumb up. Your thumb represents the axis of rotation
with north up and your curved fingers indicate the direction of rotation of our Planet.
Method: associated acute angle
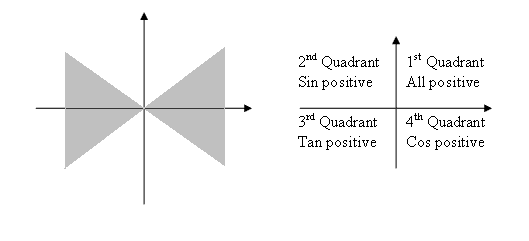
To simplify the process we use the method of the associated acute angle. This
is the angle that the line makes with the `x`-axis in the shaded part of the diagram
below on the left. We then use that angle and correct the sign using the diagram
on the right.
Example
Q: What are the exact values of `sin - 150^circ` and `tan -150^circ`?
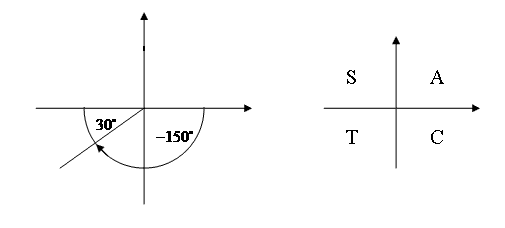
A: Associated accute angle is `180^circ - 150^circ = 30^circ`.
`sin 30^circ = 1/2` and `tan 30^circ = 1/sqrt(3).
`-150^circ` is in the 3rd quadrant so sin is negative and tan is positive.
Hence `sin - 150^circ = - 1/2` and `tan -150^circ=1/sqrt(3)`.
Exercises
- Extension of trigonometric ratios for non-acute angles: H p59 Ex 4E

- Advanced (if you get bored)
- (i) Using Pythagoras Theorem, find the equation of a circle of radius `1` (or in general radius `r`) and
prove that any point on the cicle has coordinates `(cos theta, sin theta)`.
- (ii) Reflecting on the diagram
to the right, see if you can construct a different coordinate system (i.e. a way to describe any point on the plane
with two numbers - other than the usual Cartisian coordinates).
3.4 Solving Trig Equations
Example
Q:Solve `2sin theta - 1=0` for `0 le theta < 2pi`.
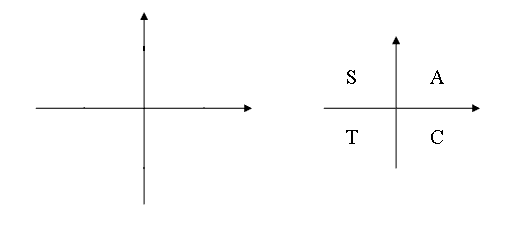
A: Rearrange the equation to get `sin theta = 1/2`. So `sin theta` is positive,
and therefore `theta` lies in the 1st and 2nd quadrants.
Associated acute angle is `sin^(-1) 1/2 = pi/6`.
In the 1st quadrant `theta = pi/6`.
In the 2nd quadrant `theta = pi - pi/6 = (5pi)/6`.
So the solutions in the range `0 le theta < 2pi` are `theta = pi/6, (5pi)/6`.
Example
Q: Solve `1=1/2 - sin 4x` for `0^circ le x le 150^circ`.

A: Rearrange the equation to get `sin 4x = - 1/2`. Since `sin 4x` is negative
there will be solutions in the 3rd and 4th quadrants.
The associated acute angle is `sin^(-1) = 30^circ`.
In the 3rd quadrant `4x = 180^circ + 30^circ = 210^circ`.
In the 4th quadrant `4x = 360^circ - 30^circ = 330^circ`.
Since `0^circ le x le 150^circ` we are looking for values of `4x` in the range `0^circ
le
4x le 600^circ`.
- `210^circ + 360^circ = 570^circ qquad qquad` In range
- `330^circ + 360^circ = 690^circ qquad qquad` Not in range so no further solutions
So `4x = 210^circ, 330^circ, 570^circ`.
Therefore `x = 52.5^circ, 82.5^circ, 142.5^circ`.
3.5 Trig with non-right angled triangles
Can only use soh-cah-toa with right-angled triangles.
But for non-right-angled triangles we have:
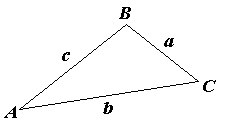
- Cosine rule
- `a^2 = b^2 + c^2 - 2bc cos A`
- Sine rule
- `a/(sin
A) = b/(sin B) = c/(sin C)`
Example
Q: What is the size of the angle `A` in the diagram?
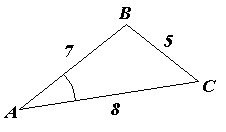
A: Use the cosine rule with `a=5`, `b=8` and `c=7`. So
- `25 = 49 +64 - 2 times 7 times 8 cos A`
- `-88 = -112 cos A`
- `cos A = 88/112 = 11/14`
Therefore `A=38.2^circ qquad` (1 d.p.)
Exercises
- Simple trigonometric equations: H p63 Ex 4H
- Simple trigonometric equations: H p65 Ex 4J (Mixed Questions)
- Sine and Cosine rules: H p338 Ex 15
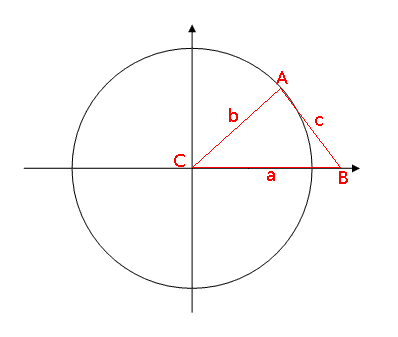
- Advanced (if you get bored)
- Let ABC be a triangle with `B=(a,0)`, `C=(0,0)` and sides `a`, `b` and `c` respectively.
- (i) By
considering the circle through the point `A` with centre at `C`, find the coordinates of the point `A`.
- (ii)
By calculating the distance between the points `A` and `B` and using the identity `cos^2 theta + sin^2 theta = 1`
prove the Cosine Rule: `c^2 = a^2 + b^2 -2ab cos C`.
Previous Exercises
- Extension of trigonometric ratios for non-acute angles: H p59 Ex 4E
- Radians: H p56; Ex 4C
- Sine / Cosine / Tangent: H p337; Ex 14
- Special Angles: H p57; Ex 4D
- Special Angles: H p59; Ex 4E
3.6 Graphs of trig functions