James Gray

University of Edinburgh

Applicable Mathematics (Foundation) af0

8: Sequences and Recurrence Relations

Exercises

8.1 Recurrence Relations

For a number `c` and a function `f`

`u_0=c` and `u_(n+1) = f(u_n)`

is a recurrence relation description of a sequence.

Exercises

More Complex Example

Q: A patient is injected with `160`ml of a drug.  Every `6` hours `25%` of the drug passes out of her bloodstream.  To compensate a further `20`ml dose is given every `6` hours.

A:  (a) Let `u_n` be the amount of drug in bloodstream after `6 times n` hours.

Initial amount `u_0 = 160`ml

After every `6` hours `25%` leaves so `75%` remains.

To the remaining `75%` an extra `20`ml is added.  So

`u_(n+1) = 75/100 u_n +20`.

(b) The patient will have received two injections after `12` hours.  So we need to calculate `u_2`.

`u_1 = 75/100 times 160 +20 = 140`ml

`u_2 = 75/100 times 140 + 20 = 125`ml

Linear Recurrence Relations

A sequence defined by

`u_(n+1) = a u_n +b \ \ \ \ \ \ \ \ \ \ \ a!=0`

is called a linear recurrence relation.

(Linear because comparing with `u_(n+1)=f(u_n)`, we see `f(x) = ax+b`, the equation of a line.)

Exercises

8.2 Sequences

A sequence in mathematics is an ordered list.  For example

`9, 9, 9`

`6,7,6,6,9`

`1,1,2,3,5,8, ldots`

`1,3,5,7, ldots`

`0, 1/2, 2/3, 3/4, ldots`

`1,-1,1,-1, ldots`

We often relate a sequence to a general sequence `u_0, u_1, u_2, ldots`

e.g. `u_0 =1, u_1=3, u_2=5`.

Note

Because we start with `u_0`, the `n`th term in the sequence is `u_(n-1)`.

Aside: Fibonacci Sequence

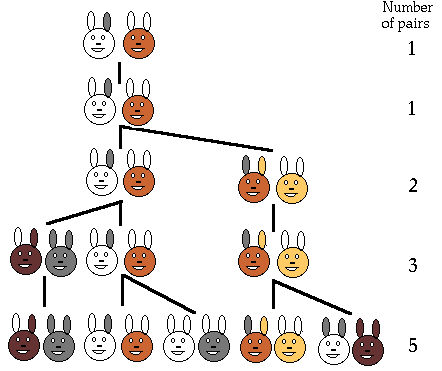
In one of Fibonacci's books he posed the following problem: "How many pairs of rabbits would there be each month if you started with a pair of newborn rabbits?"

Picture from http://www.ee.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibnat.html

Convergence and Divergence

Sometimes by plotting the points of an infinite sequence we can see patterns.

Convergence and divergence graphs

In graphs 2 to 4 there are patterns and in 2 and 3 there is a special type of pattern: convergence.

As we go further through the sequence the terms are approaching a fixed value, called the limit.

If a sequence converges it has a limit.

A sequence that doesn't converge is said to diverge.

Convergence and Recurrence Relations

Maple example

with(LREtools):
 prob := REcreate(
 u(n+1)=0.3*u(n)- 11
 ,u(n),{u(0) = 8}):
 rec := REtoproc(prob): first:= rec(0); second := rec(1); third:= rec(2); tenth := rec(9); hundreth := rec(99);
 REplot(prob,0..3);

For a linear recurrence relation 

`u_(n+1) = au_n +b`, 

if `-1 <a<1`, then the sequence `u_0, u_1, ldots` converges and has limit 

`L = b/(1-a)`.

Example

Q: Find the first four terms and the limit, if it exists, for the following recurrence relations:

(a) `quad u_(n+1) = 0.3u_n +11 qquad qquad u_0=8`

(b) `quad u_(n+1)=7-1.2u_n qquad qquad u_0=1`

A: (a) `u_0=8, u_1=13.4, u_2=15.02, u_3=15.506, ldots `

Sequence converges because `a= 0.3` and so `-1<a<1`.

Therefore limit is `L= b/(1-a)=11/(1-0.3)=15.71428 ldots`

A: (b) `u_0=1, u_1=5.8, u_2=0.04, u_3=6.952`

Sequence does not satisfy the convergence condition above, because `a=-1.2<-1`.  And by checking with a plot we see that it diverges.

8.3 Problems with Linear Recurrence Relations

Example

Q: A recurrence relation is defined by `u_(n+1) = au_n+b` has

`u_1=2, qquad u_2=4, qquad, u_3=14`.

Find `a` and `b`.

A: Because `u_(n+1) = au_n+b`, we know that `u_2 = au_1 +b` and `u_3=au_2+b`.  So using the information given in the question we get the simultaneous equations

`4=2a+b`

`14=4a+b`

Subtracting the two equations above gives `10=2a`. So `a=5`.

Substituting `a=5` into `4=2a+b`, gives `4=2 times 5 +b`.  So `b=-6`.

Example

Q: The population of Scotland is approximately 5 million. Each year since 1990, `30%` of the rural community has moved to an urban environment, while `2%` of urban dwellers have moved to the country.  Demographers are concerned with the long-term effect on the population if this pattern continues.

(a) If `R_n` denotes the rural population, in millions, after `n` years, show that 

`R_(n+1)=0.68R_n+0.1`.

(b) What would be the long-term effect on the rural population if this pattern were to continue?

A: (a) We have that `R_n=` the rural population, in millions, after `n` years.

So let `U_n=` the urban population, in millions, after `n` years.

So `R_n+U_n=5`.  That is `U_n=5-R_n`.

The information in the question also tells us that

`R_(n+1) = 0.7 R_n +0.02U_n`.

Now substitute `U_n=5-R_n` into the equation above to get

`R_(n+1) = 0.7 R_n + 0.02 (5-R_n)`

`=0.68R_n +0.1`.

(b) Comparing with the general formula for a linear recurrence relation (`u_(n+1) = au_n +b`)  we see that `a=0.68`.  Therefore the sequence converges because `-1<a<1`.

Limit `= b/(1-a) = 0.1/(1-0.68)=0.3125`

The long-term effect is that the rural population will tend to 312,500.

Exercises

  • Limits: H p78 Ex 5H
    • Q1 (a), (c), (e), (g), (i)
    • Then other odd questions
  • Find `a` and `b`: H p79 Ex 5I
    • Q1 (a), (c), (e), (h)
    • Q2
    • Q4
  • Linked R.R.: H p81 Ex 5J
    • Odd Questions

8.4 Arithmetic and Geometric Progressions

Arithmetic Sequences

Example of an arithmetic sequence: `1,4,7,10, ldots`.

The recurrence relation description is `\ \ \ u_0 = a, \ \ \ \ \ \ \ \ \ \ \ u_(n+1) = u_n+d`.

Hence the sequence is

`u_0=a ,`

`u_1=a+d ,`

`u_2=a+2d, \ .....`

So we can describe the sequence directly by `\ \ \ \ \ \ \ u_n=a+nd`.


Geometric Sequences

Example of a geometric sequence

The recurrence relation description is `\ \ \ u_0= a \ \ \ \ \ \ \ \ \ \ \ u_(n+1)=r u_n`

Hence the sequence is

`u_0 = a, `

`u_1=ra,`

`u_2 = r^2a, . . . . . `

So we can describe the sequence directly by `\ \ \ \ u_n = r^na`.